|
1、关于保证起手3张牌(包括换牌)里至少有2张前期用的牌概率问题
首先在我的模型下,什么是前期用的牌(以下称A类牌)包括,1~3费仆从(不包括过牌类、沉默类、以及成长类),4费以下(不包括4费)法术及武器。有些比较特殊的随从如TC130等,只要其下限能满足前期压制的牌都算前期的牌,这样大家就可以对号入座啦。这个概率并不难算,其函数为Z==1-(0.6*(1-X)^5+(1-X)^6),X代表A类牌在手牌中所占的概率;Z表示标题的概率。得出这样的结果:
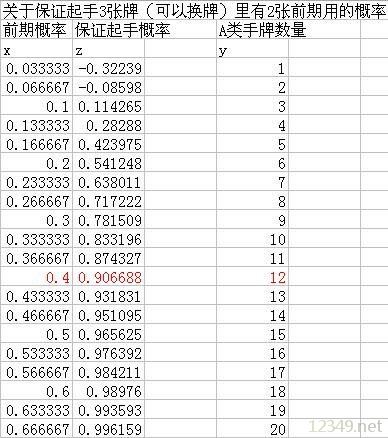
从上图可以看出,当A类手牌数量达到12张时,Z有90%的概率,换句话说,当你A类手牌达到12张时,对战十局中只会出现一局会前期卡手,并且这只是先手概率,后手概率会更高。在JJC12胜封顶的环境下,这概率完全可以接受。姑且称之为“12定律”。这是这篇文章最大的结论,但是大家要记住的是,12张是一个上限,即系话,A类牌不要超过12张,在AOE多的情况下可以更少。记住本文讨论的是如何保证前期不亏的情况下,压缩低费仆从的数量。另外补充经验之谈的是,在1~3费的选择中,想更好的压制,是保证2费拔高,3费少拿,除了麦田、血色、苦痛、大地之环外,其他不要。
2、4费问题
30张牌减去12张A类牌,剩下18张牌,假设AOE类两张,过牌类两张,硬解软解两张(C类牌),还剩下12张牌,就是4费以上仆从的数量。4费(B类牌),这个费用很特殊,一般2费仆从可以换3费仆从,但3费仆从大多换不了4费仆从。正因为这个特殊性,后手一般都会在3费跳银币来抢占主动。在这里我们单独拿出来讨论。现在我们建立一个“卡手”模型,在保证12张A类牌的前提下,当4费阶段时,保证至少一张4费牌的概率。其函数为Z2= =1-(1-X2)^5,X2代表B类牌在手牌中所占的概率;Z2表示保证至少一张4费牌的概率。得出这样的结果:
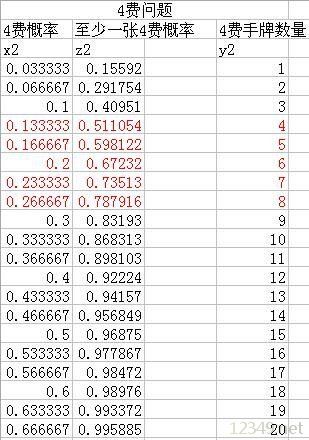
这里引入一个接受范围的问题,就比如说我们对前期压制的接受范围是90%以上,那么根据卡手模式在越往后越不重要的特点,其实这里很容易理解,只要过渡到高费阶段,就没所谓卡手的问题,那么我们的接受范围会逐步降低。所以大胆假设4费接受范围是80%以上,5费接受范围是70%以上,从上图可以看出,当B类牌有8张时,有约80%的概率不卡手,就是说5局有一局卡手,那么B类牌为8张。这就是我们的第二结论。
|
|||||